Aaltoputkien teoria

Tämä artikkeli menee syvälle aaltoputkien matematiikassa. Etenkin jos Maxwell ja osittaisdifferentiaalit ovat ystäviäsi, astu rohkeasti eteenpäin. Vaikka ne eivät oliskaan ystäviäsi, tästä pitäisi saada pohjaymmärrystä siihen, miksi lopputuloksena olevat yhtälöt ovat sellaisia kuin ovat.

Tiivistettyjä lopputuloksia esitetään "Teoria" nimisessä osassa aaltoputki artikkelissa.

Englanninkielinen termi aaltoputkelle on: waveguide, koska se ohjaa (guide) sähkömagneettista energiaa sisällään.

Yleistä

Sähkömagneettista tehoa voidaan siirtää ontossa johdeputkessa. Kun sähkömagneettista kenttää rajoitetaan tällä tavalla, sen etenemistavat poikkeavat vapaan avaruuden tilanteesta. Johtavat seinämät sallivat sähkömagneettisen kentän olemassaolon vain kun johteen pintaa pitkin ei ole sähkökenttää. Aaltoputken ominaisuudet riippuvat täten sen muodosta ja koosta. Erilaiset epäjatkuvuudet aaltoputkessa muuttavat sen siirtolinjaominaisuuksia ja näitä ominaisuuksia voidaan käyttää tuottamaan induktiivista- tai kapasitiivista reaktanssia.

Sähkö- ja magneettikenttien kuviot ovat erilaisia eri moodeissa ja niille onkin kehitetty vakio nimistö sen mukaan, onko sähkökenttä (E) vai magneettikenttä (M) nolla etenemissuuntaan (putken pituusakseli) (T = Transversal = poikittainen) josta saadaan kolme yhdistelmää: TE, TM, TEM. Aaltoputkissa vain TE ja TM ovat mahdollisia. Näihin lisätään suffiksit (TE_mn, TM_mn), jotka kertovat että montako kertaa kyseinen kenttä muuttuu annetulla akselilla.

Merkintätapa on, että ensimmäinen numero (m) on suorakaideputken pidemmän sivun (a) suuntaan olevien puoliaaltojen määrän ja toinen (n) on lyhyemmän sivun (b).

Pyöreälle putkelle ensimmäinen numero (m) on putken sisäpinnan ympäri olevien täysien sähkökentän aaltojen määrä (ei puoliaaltojen!) ja toinen (n) on putken lävistäjän läpi olevien puoliaaltojen määrä.

Seuraavaksi kirjoitetaan Maxwellin yhtälöillä suorakulmaisen aaltoputken sisäisten kenttien olemus ensin tavallisessa oikeakätisessä suorakulmaisessa koordinaatistossa, jossa z on putken pituussuuntaan ja positiivinen signaalin etenemissuuntaan.

Pyöreän aaltoputken tarpeisiin tehdään sama harjoitus polaarikoordinaatistolla, jossa z on samoin kuin suorakulmaisella tapauksella.

Pyörittelemällä Maxwellin yhtälöitä ja kieltämällä tapaus: m = n = 0 saadaan sitten...

Suorakaideaaltoputki

Suorakaideaaltoputki on ontto metalliputki, jonka poikkileikkaus on suorakaide. Putken johtavat seinät pitävät sähkömagneettisen kentän sisällään ja näin ohjaavat niitä. Useita erilaisia sähkömagneettisten kenttien konfiguraatioita ('moodeja') voi samanaikaisesti olla olemassa aaltoputkessa.

Kun sähkömagneettisen kentän "aallot" kulkevat pitkin johdetta (putkea), ne heijastelevat edestakaisin seinien välillä. Tästä seuraa, että joko sähkökenttä tai magneettikenttä on etenemissuuntainen, eli se ei enää olekaan poikittainen sähkömagneettinen aalto (Transversal electromagnetic wave - TEM). Oheinen kuva esittää, miten mikä tahansa säännöllinen tasoaalto voidaan häviöttömässä johteessa esittää TE ja TM -aalloiksi.

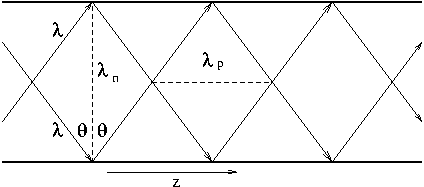
Tasoaallon heijastuminen aaltoputkessa

Kun aallonpituus $\lambda \,$ on se jaettavissa putken pituussuuntaiseen ($\lambda _{p}\,$) ja siihen nähden kohtisuoraan ('normaaliin', $\lambda _{n}\,$) yhtälöinä:

$\lambda _{n}={\frac {\lambda }{\cos \theta }}\qquad \lambda _{p}={\frac {\lambda }{\sin \theta }}\,$

(eq.1)

missä $\theta \,$ on heijastuvan aallon heijastuskulma ja $\lambda \,$ on saapuvan signaalin aallonpituus vapaassa väliaineessa (jos putkessa olisi jotain muuta kuin ilmaa/tyhjöä.)

Aaltoputkessa oleva tasoaalto on nähtävissä kahtena komponenttina: ensimmäinen on seisova aalto joka on kohtisuorassa putken heijastavia seiniä kohtaan ja toinen on liikkuva aalto joka kulkee heijastavien seinien kanssa samaan suuntaan. Häivöttömässä aaltoputkessa nämä etenemistila (moodit) voidaan luokitella olemaan joko transverse electric (TE), tai transverse magnetic (TM).

Suorakaideputkissa näitä moodeja kutsutaan nimillä: TE_mn ja TM_mn, missä m laskee puolia aallonpituuksia sähkö- tai magneettikentän voimakkuuksia x-koordinaatin (yleensä suorakaideputken pidemmän sivun) suuntaan. Samoin n kertoo puolien aallonpituuksien määrän y-koordinaatin (yleensä suorakaideputken lyhyemmän sivun) suuntaan.

Aaltoyhtälöiden ratkaisuja suorakulmaisissa koordinaateissa

Aaltoyhtälöille voidaan tarjota ratkaisut sekä aika- että taajuusdomaineissa. Yksinkertaisuuden vuoksi käsittelemme nyt kuitenkin vain siniaallon vakaan tilan (steady state, tai taajuusdomain!) ratkaisuja oikeakätisessä suorakulmaisessa koordinaatistossa.

Sähköiset ja magneettiset aaltoyhtälöt voidaan esittää taajuusdomainissa seuraavin vektoriyhtälöin:

$\nabla ^{2}\mathbf {E} =\,$	$\gamma ^{2}\mathbf {E}$	(eq.2-E)
$\nabla ^{2}\mathbf {H} =$	$\gamma ^{2}\mathbf {H}$	(eq.2-H)

jossa:

$\gamma ={\sqrt {j\omega \mu \left(\sigma +j\omega \epsilon \right)}}=\alpha +j\beta$

(eq.3)

Suorakulmaisissa (ja yleensä oikeakätisissä) koordinaateissa lausuttavat E tai H noudattavat kompleksista skalaariaaltoyhtälöä, alias Helmholtzin yhtälöä.

$\nabla ^{2}\psi =\gamma ^{2}\psi$

(eq.4)

Helmholtzin yhtälö suorakulmaisissa koordinaateissa on:

${\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}=\gamma ^{2}\psi$

(eq.5)

Tämä on lineaarinen ja homogeeninen osittaisdifferentiaaliyhtälö kolmessa ulottuvuudessa. Käyttämällä muuttujien erottelua, ratkaisuksi saadaan:

$\psi =X\left(x\right)Y\left(y\right)Z\left(z\right)$

(eq.6)

missä esim. $X\left(x\right)$ on funktio pelkän x-koordinaatin suhteen.

Sijoittamalla yhtälö (eq.6) yhtälöön (eq.5) ja jakamalla tulos yhtälöllä (eq.6), saadaan:

${\frac {1}{X}}{\frac {d^{2}X}{dx^{2}}}+{\frac {1}{Y}}{\frac {d^{2}Y}{dy^{2}}}+{\frac {1}{Z}}{\frac {d^{2}Z}{dz^{2}}}=\gamma ^{2}$

(eq.7)

Koskapa edellisten kolmen termin summa on vakio ja jokainen niistä termeistä on oma itsenäinen riippumaton muuttuja, jokaisen osatermin pitää olla vakion kokoinen.

Olkoot yllä olevat kolme termiä: $k_{x}^{2},k_{y}^{2},k_{z}^{2}\,$, osittaisdifferentiaalin erottelu voidaan esittää muodossa:

$-k_{x}^{2}-k_{y}^{2}-k_{z}^{2}=\gamma ^{2}\,$

(eq.8)

Yleinen ratkaisu kullekin (eq.7) differentiaaliyhtälölle on:

${\frac {d^{2}X}{dx^{2}}}=\,$	$-k_{x}^{2}X\,$	(eq.9-x)
${\frac {d^{2}Y}{dy^{2}}}=\,$	$-k_{y}^{2}Y\,$	(eq.9-y)
${\frac {d^{2}Z}{dz^{2}}}=\,$	$-k_{z}^{2}Z\,$	(eq.9-z)

ja ne ovat käännettävissä muotoon:

$X=\,$	$A\sin k_{x}x+B\cos k_{x}x\,$	(eq.10-x)
$Y=\,$	$C\sin k_{y}y+D\cos k_{y}y\,$	(eq.10-y)
$Z=\,$	$E\sin k_{z}z+F\cos k_{z}z\,$	(eq.10-z)

Suorakulmaisissa koordinaateissa Helmholtz yhtälöjen täydet ratkaisut ovat näin ollen:

$\psi =\,$	$\left(A\sin k_{x}x+B\cos k_{x}x\right)\left(C\sin k_{y}y+D\cos k_{y}y\right)\,$
	$\times \left(E\sin k_{z}z+F\cos k_{z}z\right)\,$	(eq.11)

Aaltojen eteneminen aaltoputkessa ajatellaan konvention mukaan olevan positiiviseen z-koordinaatin suuntaan. On myöskin huomiolle pantavaa, että aaltoputken etenemisvakio $\gamma _{g}\,$ putkessa poikkeaa putkea täyttävän väliaineen etenemisvakiosta ($\gamma \,$). Olkoot:

$\gamma _{g}^{2}=\gamma ^{2}+k_{x}^{2}+k_{y}^{2}=\gamma ^{2}+k_{c}^{2}$

(eq.12)

missä

$k_{c}={\sqrt {k_{x}^{2}+k_{y}^{2}}}$

(eq.13)

yleensä tämä tunnetaan termillä cutoff wave number.

Häviöttömälle eristeelle/täyteaineelle käytämme sijoitusta $\gamma ^{2}=-\omega ^{2}\mu \epsilon \,$ ja saamme:

$\gamma _{g}=\pm j{\sqrt {\omega ^{2}\mu \epsilon -k_{c}^{2}}}$

(eq.14)

Etenemävakiolle $\gamma _{g}\,$ aaltoputkissa saamme kolme eri tapausta:

Tapaus 1:

Aallon etenemistä ei tapahdu (vaan voimakasta häipymistä) jos $\omega _{c}^{2}\mu \epsilon =k_{c}^{2}\,$ ja $\gamma _{g}=0\,$. Edellä oleva on ns. kriittinen raja alarajataajuudelle ja se voidaan muotoilla:

$f_{c}={\frac {1}{2\pi {\sqrt {\mu \epsilon }}}}{\sqrt {k_{x}^{2}+k_{y}^{2}}}$

(eq.15)

Tapaus 2:

Aaltomuoto etenee putkessa, jos $\omega ^{2}\mu \epsilon >k_{c}^{2}\,$ ja:

$\gamma _{g}=\pm j\beta _{g}=\pm j\omega {\sqrt {\mu \epsilon }}{\sqrt {1-\left(f_{c}/f\right)^{2}}}$

(eq.16)

Tämä merkitsee, että taajuuden pitää olla alarajan yläpuolella, jotta aaltomuoto etenisi putkessa.

Tapaus 3:

Aaltomuoto vaimenee, jos $\omega ^{2}\mu \epsilon <k_{c}^{2}\,$ ja:

$\gamma _{g}=\pm \alpha _{g}=\pm \omega {\sqrt {\mu \epsilon }}{\sqrt {\left(f_{c}/f\right)^{2}-1}}$

(eq.17)

joka kertoo, että operoitaessa taajuudella joka on alarajan alapuolella, aaltomuoto vaimenee eksponentiaalisesti suhteessa tekijään $-\alpha _{g}z\,$, eikä aaltomuoto etene, koska etenemisvakio on reaaliluku.

Siksi ratkaisuksi Helmholtzin yhtälölle suorakulmaisissa koordinaateissa voidaan muotoilla:

$\psi =\left(A\sin k_{x}x+B\cos k_{x}x\right)\left(C\sin k_{y}y+D\cos k_{y}y\right)e^{-j\beta _{g}z}\,$

(eq.18)

TE-muodot suorakulmaisessa aaltoputkessa

Käytämme edelleen oletusta, että aaltomuodot etenevät positiiviseen z-akselin suuntaan oikeakätisessä suorakulmaisessa koordinaatistossa.

TE_mn-etenemismuotojen ominaispiirre aaltoputkessa on, että $E_{z}=0\,$. Toisin sanoen, magneettikentän z-komponentin, $H_{z}\,$, pitää olla olemassa, että energiaa siirtyisi putkessa. Seuraten edellä mainitusta Helmholtzin yhtälöstä:

$\nabla ^{2}H_{z}=\gamma ^{2}H_{z}\,$

(eq.19)

jolle saadaan ratkaisu joka on muotoa:

$H_{z}=\,$	$\left(A_{m}\sin {\frac {m\pi x}{a}}+B_{m}\cos {\frac {m\pi x}{a}}\right)$
	$\times \left(C_{n}\sin {\frac {n\pi y}{b}}+D_{n}\cos {\frac {n\pi y}{b}}\right)e^{-j\beta _{g}z}$	(eq.20)

jota rajoittavat annetut rajaehdot, missä: $k_{x}=m\pi /a\,$ ja $k_{y}=n\pi /b\,$ sijoitettiin yhtälöön. Häivöttömälle eristeelle Maxwellin curl-yhtälöt taajuusdomainissa ovat:

$\nabla \times \mathbf {E} =\,$	$-j\omega \mu \mathbf {H} \,$	(eq.21-E)
$\nabla \times \mathbf {H} =\,$	$j\omega \epsilon \mathbf {E} \,$	(eq.21-H)

suorakulmaisissa koordinaateissa niiden komponentit ovat:

${\frac {\partial E_{z}}{\partial y}}-{\frac {\partial E_{y}}{\partial z}}=$	$-j\omega \mu H_{x}\,$	(eq.22-Hx)
${\frac {\partial E_{x}}{\partial z}}-{\frac {\partial E_{z}}{\partial x}}=$	$-j\omega \mu H_{y}\,$	(eq.22-Hy)
${\frac {\partial E_{y}}{\partial x}}-{\frac {\partial E_{x}}{\partial y}}=$	$-j\omega \mu H_{z}\,$	(eq.22-Hz)
${\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}=$	$j\omega \epsilon E_{x}\,$	(eq.22-Ex)
${\frac {\partial H_{x}}{\partial z}}-{\frac {\partial H_{z}}{\partial x}}=$	$j\omega \epsilon E_{y}\,$	(eq.22-Ey)
${\frac {\partial H_{y}}{\partial x}}-{\frac {\partial H_{x}}{\partial y}}=$	$j\omega \epsilon E_{z}\,$	(eq.22-Ez)

Sijoittamalla edellisiin yhtälöihin $\partial /\partial z=-j\beta _{g}\,$ ja $E_{z}=0\,$, saadaan yksinkertaisemmat yhtälöt:

$\beta _{g}E_{y}=\,$	$-\omega \mu H_{x}\,$	(eq.23-Hx)
$\beta _{g}E_{x}=\,$	$\omega \mu H_{y}\,$	(eq.23-Hy)
${\frac {\partial E_{y}}{\partial x}}-{\frac {\partial E_{x}}{\partial y}}=$	$-j\omega \mu H_{z}\,$	(eq.23-Hz)
${\frac {\partial H_{z}}{\partial y}}+j\beta _{g}H_{y}=\,$	$j\omega \epsilon E_{x}\,$	(eq.23-Ex)
$-j\beta _{g}H_{x}-{\frac {\partial H_{z}}{\partial x}}=$	$j\omega \epsilon E_{y}\,$	(eq.23-Ey)
${\frac {\partial H_{y}}{\partial x}}-{\frac {\partial H_{x}}{\partial y}}=$	$0\,$	(eq.23-Ez)

Ratkaisemalla näistä kuudesta yhtälöstä $E_{x},E_{y},H_{x},H_{y}\,$ muuttujan $H_{z}\,$ suhteen ja tekemällä sijoitus $k_{c}^{2}=\omega ^{2}\mu \epsilon -\beta _{g}^{2}\,$, saadaan TE-moodin kenttäyhtälöt suorakulmaisessa aaltoputkessa:

$E_{x}=\,$	${\frac {-j\omega \mu }{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial y}}$	(eq.24-Ex)
$E_{y}=\,$	${\frac {j\omega \mu }{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial x}}$	(eq.24-Ey)
$E_{z}=\,$	$0\,$	(eq.24-Ez)
$H_{x}=\,$	${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial x}}$	(eq.24-Hx)
$H_{y}=\,$	${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial y}}$	(eq.24-Hy)
$H_{z}=\,$	$\left(A_{m}\sin {\frac {m\pi x}{a}}+B_{m}\cos {\frac {m\pi x}{a}}\right)$	(eq.20)(eq.24-Hz)
	$\times \left(C_{n}\sin {\frac {n\pi y}{b}}+D_{n}\cos {\frac {n\pi y}{b}}\right)e^{-j\beta _{g}z}$

Differentioimalla yhtälö (eq.24-Hz) x:n ja y:n suhteen ja sitten sijoittamalla tulokset muista (eq.24) ryhmän yhtälöistä siihen, saadaan varsinaiset kenttäyhtälöt.

Rajatilojen määritykset sovitetaan saatuihin uusiin yhtälöihin siten, että joko E-kentän tangentti, tai H-kentän normaali katoaa johteiden pinnoilla. Koska silloin $E_{x}=0\,$, on $\partial H_{z}/\partial y=0$ kun y = 0 tai b. Siten $C_{n}=0\,$. Koskapa $E_{y}=0\,$ silloin $\partial H_{z}/\partial x=0$ kun x = 0 tai a. Siten myös $A_{m}=0\,$.

Noin ylipäätään voidaan vetää johtopäätös, että $H_{z}\,$:n normaalin derivaatan pitää kadota johtavalla pinnalla, eli johteen seinillä:

${\frac {\partial H_{z}}{\partial n}}=0$

(eq.25)

Tästä seuraa, että magneettikenttä positiiviseen z-akselin suuntaan voidaan kirjoittaa muotoon:

$H_{z}=H_{0z}\cos {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$

(eq.26)

missä $H_{0z}\,$ on amplitudivakio.

Sijoittamalla yhtälö (eq.26) ryhmän (eq.24) yhtälöihin, saadaan TE_mn kenttäyhtälöt suorakulmaisessa aaltoputkessa:

$E_{x}=\,$	$E_{0x}\cos {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.27-Ex)
$E_{y}=\,$	$E_{0y}\sin {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.27-Ey)
$E_{z}=\,$	$0\,$	(eq.27-Ez)
$H_{x}=\,$	$H_{0x}\sin {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.27-Hx)
$H_{y}=\,$	$H_{0x}\cos {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.27-Hy)
$H_{z}=\,$	$H_{0z}\cos {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.26)(eq.27-Hz)

edellä m ja n ovat ei-negatiivisia kokonaislukuja, mutta arvo m = n = 0 ei ole sallittu.

---

Aloitetaan koostamaan muutamia strategisia yhtälöitä:

Apumuuttuja:

$v_{p}={\frac {1}{\sqrt {\mu \epsilon }}}={\frac {c}{\sqrt {\mu _{r}\epsilon _{r}}}}$

(eq.28)

on signaalin vaihenopeus putken sisäisessä eristemateriaalissa, ilmalle/tyhjölle se on valonnopeus.

Yhtälön (eq.12) mukaan ns. Cutoff wave number on:

$k_{c}={\sqrt {\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}}$	$=\omega _{c}{\sqrt {\mu \epsilon }}$	(eq.29)
	$\,\,={\frac {2\pi f_{c}{\sqrt {\mu _{r}\epsilon _{r}}}}{c}}$	(eq.30)

jossa a ja b on metreinä.

Yhtälön (eq.15) mukaan aaltoputken alarajataajuus on:

$f_{c}={\frac {1}{2{\sqrt {\mu \epsilon }}}}{\sqrt {{\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}}}={\frac {1}{2}}v_{p}{\sqrt {{\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}}}$

(eq.31)

jota vastaava aallonpituus:

$\lambda _{c}={\frac {2}{\sqrt {\left({\frac {m}{a}}\right)^{2}+\left({\frac {n}{b}}\right)^{2}}}}$

(eq.32)

Huomio: Tämä ei riipu putken täyteaineen ominaisuuksista !

Etenemisvakio (tai tässä vaihevakio) kuten yhtälö (eq.14) sen ilmaisee on lausuttavissa muodossa:

$\beta _{g}=\omega {\sqrt {\mu \epsilon }}{\sqrt {1-\left(f_{c}/f\right)^{2}}}$

(eq.33)

Vaihenopeus positiivizeen z-akselin suuntaan:

$v_{g}={\frac {\omega }{\beta _{g}}}={\frac {v_{p}}{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.34)

Ominaisaaltoimpedanssi TE-moodeille voidaan lausua yhtälöistä (eq.23-Hx ja eq.23-Hy) johtamalla muotoon:

$Z_{g}={\frac {E_{x}}{H_{y}}}=-{\frac {E_{y}}{H_{x}}}={\frac {\omega \mu }{\beta _{g}}}={\frac {\eta }{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.35)

missä: $\eta ={\sqrt {\mu /\epsilon }}$ on eristeen ominaisimpedanssi.

Aaltoputken aallonpituus on:

$\lambda _{g}={\frac {\lambda }{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.36)

missä: $\lambda =v_{p}/f\,$ on aallonpituus putken sisäeristeessä.

TM-aaltoputkimoodit suorakaideputkelle

TM_mn-etenemismuotojen ominaispiirre aaltoputkessa on, että $H_{z}=0\,$. Toisin sanoen, sähkökentänkentän z-komponentin, $E_{z}\,$, pitää olla olemassa, että energiaa siirtyisi putkessa. Seuraten edellä mainitusta, Helmholtzin yhtälöstä tulee:

$\nabla ^{2}E_{z}=\gamma ^{2}E_{z}\,$

(eq.37)

jolle saadaan ratkaisu joka on muotoa:

$E_{z}=\,$	$\left(A_{m}\sin {\frac {m\pi x}{a}}+B_{m}\cos {\frac {m\pi x}{a}}\right)\,$
	$\left(C_{n}\sin {\frac {n\pi y}{b}}+D_{n}\cos {\frac {n\pi y}{b}}\right)e^{-j\beta _{g}z}\,$	(eq.38)

jonka varsinaista ratkaisua varten sitä täytyy rajoittaa rajapintaehdoilla. Tämä on samanlaista, kuin TE-moodien haku.

Rajapintaehto $E_{z}\,$ vaatii, että kenttä häviää (nollaan) aaltoputken seinillä, koska sähkökentän tangenttikomponentin ($E_{z}\,$) tulee olla nolla johtavalla pinnalla. Näin ollen koska $E_{z}=0\,$ kun $x=0,a\,$, silloin $B_{m}=0\,$. Samoin $E_{z}=0\,$-ehto reunoilla 0, b pakottaa: $D_{n}=0\,$. Näin yhtälö (eq.38) pelkistyy muotoon:

$E_{z}=E_{0z}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$

(eq.39)

missä $m=1,2,3,\dots \quad n=1,2,3,\dots$.

Jos m tai n ovat nollia, kentät vaimenevat nollaan. Siksi suorakulmaisessa putkessa ei ole TM₀₁ tai TM₁₀ -moodeja, jonka vuoksi TE₁₀-moodi on dominoiva suorakulmaisessa putkessa, jonka a > b.

Tapaukselle $H_{z}=0\,$ saadaan kenttäyhtälöt laventamalla $\nabla \times \mathbf {H} =j\omega \epsilon \mathbf {E}$:

${\frac {\partial E_{z}}{\partial y}}+j\beta _{g}E_{y}=\,$	$-j\omega \mu H_{x}\,$	(eq.40-Hz)
$j\beta _{g}E_{x}+{\frac {\partial E_{z}}{\partial x}}=\,$	$j\omega \mu H_{y}\,$	(eq.40-Hy)
${\frac {\partial E_{y}}{\partial x}}-{\frac {\partial E_{x}}{\partial y}}=\,$	$0\,$	(eq.40-Hx)
$\beta _{g}H_{y}=\,$	$\omega \epsilon E_{x}\,$	(eq.40-Ex)
$-\beta _{g}H_{x}=\,$	$\omega \epsilon E_{y}\,$	(eq.40-Ey)
${\frac {\partial H_{y}}{\partial x}}-{\frac {\partial H_{x}}{\partial y}}=\,$	$j\omega \epsilon E_{z}\,$	(eq.40-Ez)

Näiden yhtälöiden samanaikainen ratkaisu $E_{z}\,$:n suhteessa muuttujille $E_{x},E_{y},H_{x},H_{y}\,$ ja tekemällä sijoitus $\beta _{g}^{2}-\omega ^{2}\mu \epsilon =-k_{c}^{2}\,$, saadaan kenttäyhtälöt TM-moodeille:

$E_{x}=\,$	${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial x}}$	(eq.41-Ex)
$E_{y}=\,$	${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial y}}$	(eq.41-Ey)
$E_{z}=\,$	$E_{0z}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.41-Ez)(eq.39)
$H_{x}=\,$	${\frac {j\omega \epsilon }{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial y}}$	(eq.41-Hx)
$H_{y}=\,$	${\frac {-j\omega \epsilon }{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial x}}$	(eq.41-Hy)
$H_{z}=\,$	$0\,$	(eq.41-Hz)

Differentoimalla edellä olevat yhtälöt x:n ja y:n suhteen sekä sijoittamalla tulokseen yhtälöiden (eq.41) tulokset saadaan varsinaiset TM_mn-moodin kenttäyhtälöt suorakulmaisessa aaltoputkessa muotoon:

$E_{x}=\,$	$E_{0x}\cos {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.42-Ex)
$E_{y}=\,$	$E_{0y}\sin {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.42-Ey)
$E_{z}=\,$	$E_{0z}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.42-Ez)(eq.39)
$H_{x}=\,$	$H_{0x}\sin {\frac {m\pi x}{a}}\cos {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.42-Hx)
$H_{y}=\,$	$H_{0y}\cos {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}e^{-j\beta _{g}z}$	(eq.42-Hy)
$H_{z}=\,$	$0\,$	(eq.42-Hz)

Useimmat TM-moodin ominaisyhtälöistä ovat identtisiä TE-moodin kanssa, mutta yksi poikkeuskin on:

Alarajataajuus $f_{c}$ on kuten TE-moodilla yllä.

Etenemisvakio $\beta _{g}\,$ on kuten TE-moodilla yllä.

Vaihenopeus $v_{g}\,$ on kuten TE-moodilla yllä.

Ominaisaaltoimpedanssi TM-moodeille voidaan lausua:

$Z_{g}={\frac {\beta _{g}}{\omega \epsilon }}=\eta {\sqrt {1-\left(f_{c}/f\right)^{2}}}$

(eq.43-Zg)

missä: $\eta ={\sqrt {\mu /\epsilon }}$ on eristeen ominaisimpedanssi kuten TE-moodilla.

Aaltoputken aallonpituus $\lambda _{g}\,$ on kuten TE-moodilla.

Tehon siirto suorakulmaisessa aaltoputkessa

Aaltoputkessa siirrettävä teho ja putken seinämähäviöt voidaan laskea kompleksisessa Poynting teoreemalla. Lähtökohtana pidetään tilannetta, jossa aaltoputki on äärettömän pitkä suhteessa aallonpituuteen ja että se on päätetty ideaaliseen kuormaan siten, ettei päistä tule heijastuksia. Aaltoputkessa siirrettävä teho on lausuttavissa:

$P_{tr}=\oint \mathbf {p} \cdot d\mathbf {s} =\oint {\frac {1}{2}}\left(\mathbf {E} \times \mathbf {H*} \right)\cdot d\mathbf {s}$

(eq.44)

Häviöttömälle eristeelle saadaan aaltoputken läpi kulkevan tehon aika-keskiarvo lausuttua:

$P_{tr}={\frac {1}{2Z_{g}}}\int _{a}\left|E\right|^{2}\,da={\frac {Z_{g}}{2}}\int _{a}\left|H\right|^{2}\,da$

(eq.45)

missä:

$Z_{g}={\frac {E_{x}}{H_{y}}}=-{\frac {E_{y}}{H_{x}}}$

$\left|E\right|^{2}=\left|E_{x}\right|^{2}+\left|E_{y}\right|^{2}$

$\left|H\right|^{2}=\left|H_{x}\right|^{2}+\left|H_{y}\right|^{2}$

Näin TE_mn-moodeille on keskimääräinen suorakaideaaltoputken läpi kulkeva teho:

$P_{tr}={\frac {\sqrt {1-\left(f_{c}/f\right)^{2}}}{2\eta }}\int _{0}^{b}\int _{0}^{a}\left(\left|E_{x}\right|^{2}+\left|E_{y}\right|^{2}\right)\,dx\,dy$

(eq.46-TE)

Vastaavasti TM_mn-moodeille se on:

$P_{tr}={\frac {1}{2\eta {\sqrt {1-\left(f_{c}/f\right)^{2}}}}}\int _{0}^{b}\int _{0}^{a}\left(\left|E_{x}\right|^{2}+\left|E_{y}\right|^{2}\right)\,dx\,dy$

(eq.46-TM)

edellä $\eta ={\sqrt {\mu /\epsilon }}$ on eristeaineen ominaisimpedanssi.

Tehohäviö suorakulmaisessa aaltoputkessa

Suorakulmaisessa aaltoputkessa on kahdenlaisia häviöitä:

1. eristeaineen häviöt
2. putken seinien ohmiset häviöt

Eristeaineen häviöt

Aloitetaan asian tarkastelu putkea täyttävän eristeaineen (tyhjön/ilman) häivöistä. Pienihäviöisen rajattoman eristeaineen (missä $\sigma <\!\!<\mu \epsilon \,$) tasoaallon etenemisvakio voidaan esittää:

$\alpha ={\frac {\sigma }{2}}{\sqrt {\frac {\mu }{\epsilon }}}={\frac {\eta \sigma }{2}}$

(eq.47)

Näin suorakulmaisen aaltoputken eristeaineen häviöt TE_mn ja TM_mn-moodeissa ovat:

TE-mode:	$\alpha _{g}={\frac {\sigma \eta }{2{\sqrt {1-\left(f_{c}/f\right)^{2}}}}}$	(eq.48-TE)
TM-mode:	$\alpha _{g}={\frac {\sigma \eta {\sqrt {1-\left(f_{c}/f\right)^{2}}}}{2}}$	(eq.48-TM)

Taajuuden f ollessa paljon yli rajataajuuden ($f>\!\!>f_{c}\,$), vaimennusvakio $\alpha _{g}\,$ lähestyy rajattoman eristeaineen ominaisuuksia (eq.47). Mutta kun taajuus on paljon alle rajataajuuden, vaimennusvakio kasvaa erittäin suureksi ja aaltomuoto ei käytännössä etene.

Aaltoputken seinien tehohäviöt

Seuraavaksi tutkitaan aaltoputken seinissä tapahtuvia tehohäviöitä. Aaltoputkessa etenevien sähkö- ja magneettikenttien intensiteetit voidaan lausua muodossa:

$\left|E\right|=\left|E_{0z}\right|e^{-a_{g}z}$	(eq.49-E)
$\left|H\right|=\left|H_{0z}\right|e^{-a_{g}z}$	(eq.49-H)

missä $E_{0z}\,$ ja $H_{0z}\,$ ovat kenttäintensiteetit z-akselilla kohdassa $z=0\,$.

On huomionarvoista todeta, että pienihäviöisessä putkessa tehovirran aikakeskiarvo pienenee suhteessa tekijään $e^{-2\alpha _{g}z}\,$. Näin ollen:

$P_{tr}=\left(P_{tr}+P_{loss}\right)e^{-2\alpha _{g}z}\,$

(eq.50)

Erityisesti kun $P_{loss}<\!\!<P_{tr}\,$ ja $2\alpha _{g}z<\!\!<1\,$:

${\frac {P_{loss}}{P_{tr}}}+1=1+2\alpha _{g}z$

(eq.51)

Lopulta:

$\alpha _{g}={\frac {P_{L}}{2P_{tr}}}$

(eq.52)

missä $P_{L}\,$ on tehohäviö yksikköpituutta kohti.

Koskapa sähkö- ja magneettikentät aaltoputken johdepinnalla vaimenevat eksponentiaalisesti mentäessä syvemmälle seinämän aineeseen, on helpompi määritellä aaltoputken pinnan ominaisvastus:

$R_{s}\equiv {\frac {\rho }{\delta }}={\frac {1}{\sigma \delta }}={\frac {\alpha _{g}}{\rho }}={\sqrt {\frac {\pi f\mu }{\sigma }}}\quad \Omega$

(eq.53)

missä $\rho \,$ (rho) seinämän materiaalin ominaisvastus ohmi-metriä, $\sigma \,$ (sigma) johtavuus siemensseinä, $\delta \,$ (delta) tunkeumasyvyys metreinä.

Tehohäviö per pituusmittayksikkö saadaan integroimalla pituusmittayksikön matkalla johteen pinnan tehotiheys:

$P_{L}={\frac {R_{s}}{2}}\int _{s}\left|H_{t}\right|^{2}\,ds\,$

W/yksikköpituus

(eq.54)

missä $H_{t}\,$ on johteen seinällä olevan magneettikentän intensiteetin tangenttikomponentti. Sijoittamalla yhtälöt (eq.45) ja (eq.54) yhtälöön (eq.52) saadaan:

$\alpha _{g}={\frac {R_{s}\int _{s}\left|H_{t}\right|^{2}ds}{2Z_{g}\int _{a}\left|H\right|^{2}da}}$

(eq.55)

missä:

$\left|H\right|^{2}$	$=\left|H_{x}\right|^{2}$	$+\left|H_{y}\right|^{2}$	(eq.56)
$\left|H_{t}\right|^{2}$	$=\left|H_{tz}\right|^{2}$	$+\left|H_{ty}\right|^{2}$	(eq.57)

Pyöreä aaltoputki

Pyöreä aaltoputki on poikkileikkauksen muotoaan lukuunottamatta kuten suorakaideputki ja se kykenee kuljettamaan sisällään sähkömagneettista tasoaaltoa.

Muunkinlaiset poikkileikkauksen geometriat kykenevät kuljettamaan sähkömagneettista energiaa, esim. elliptiset putket.

Aaltoyhtälöt sylinterikoordinaateissa

Aivan kuten edellä suorakaideputkille, tässäkin pitäydytään vain siniaaltojen pysyvän olotilan ( = taajuusdomainin ) ratkaisujen etsintään.

Käytettävä koordinaattijärjestelmä:

• $\phi \,$ (fii): x-y -tason origon ympäri x-akselista laskettava kulma
• r: Etäisyys z-akselista
• a: aaltoputken sisäpinnan säde
• z: z-koordinaatti, l. etäisyys x-y-tasosta.

Skalaarimuotoinen Helmholtz-yhtälö sylinterikoordinaateissa saa muodon:

${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}=\gamma ^{2}\psi$

(eq.58)

Käyttäen muuttujien erottelua tämä saadaan muotoon:

$\Psi =R\left(r\right)\Phi \left(\phi \right)Z\left(z\right)\,$

(eq.59)

missä:

• $R\left(r\right)\,$ = r-koordinaatin funktio
• $\Phi \left(\phi \right)\,$ = $\phi \,$-koordinaatin funktio
• $Z\left(z\right)\,$ = z-koordinaatin funktio

Sijoittamalla yhtälö (eq.59) yhtälöön (eq.58) ja jakamalla tulos yhtälöllä (eq.59), saadaan:

${\frac {1}{rR}}{\frac {d}{dr}}\left(r{\frac {dR}{dr}}\right)+{\frac {1}{r^{2}\Phi }}{\frac {d^{2}\Phi }{d\phi ^{2}}}+{\frac {1}{Z}}{\frac {d^{2}Z}{dz^{2}}}=\gamma ^{2}$

(eq.60)

Koskapa kolmen riippumattoman termin summa on vakio, jokaisen kolmesta termistä pitää olla vakio. Asetetaan nyt kolmas termi vakioksi $\gamma _{g}^{2}\,$:

${\frac {d^{2}Z}{dz^{2}}}=\gamma _{g}^{2}Z$

(eq.61)

Yhtälön ratkaisu on muotoa:

$Z=Ae^{-\gamma _{g}z}+Be^{\gamma _{g}z}$

(eq.62)

missä $\gamma _{g}\,$ on aallon etenemisvakio aaltoputkessa.

Sijoittamalla $\gamma _{g}^{2}\,$ kolmanneksi termiksi yhtälön (eq.60) vasemmalle puolelle ja kertomalla saatu yhtälö $r^{2}\,$:lla, saadaan:

${\frac {r}{R}}{\frac {d}{dr}}\left(r{\frac {dR}{dR}}\right)+{\frac {1}{\Phi }}{\frac {d^{2}\Phi }{d\phi ^{2}}}-\left(\gamma ^{2}-\gamma _{g}^{2}\right)r^{2}=0$

(eq.63)

Tuon toinen termi on pelkästään $\phi \,$:n suhteen oleva funktio, joten sijoittamalla sen paikalle vakio: $\left(-n^{2}\right)\,$, saadaan:

${\frac {d^{2}\Phi }{d\phi ^{2}}}=-n^{2}\Phi$

(eq.64)

Tälle yhtälölle löytyy ratkaisuksi myös harmoninen funktio:

$\Phi =A_{n}\sin n\phi +B_{n}\cos n\phi \,$

(eq.65)

Korvaamalla yhtälön (eq.63) termi $\Phi \,$ termillä $\left(-n^{2}\right)\,$ ja kertomalla tulos $R\,$:llä, saadaan:

$r{\frac {d}{dr}}\left(r{\frac {dR}{dr}}\right)+\left(\left(k_{c}r\right)^{2}-n^{2}\right)R=0$

(eq.66)

tämä on n-kertaluvun Besselin-funktio, missä:

$k_{c}^{2}+\gamma ^{2}=\gamma _{g}^{2}\,$

(eq.67)

joka tunnetaan Besselin funktion ominaisyhtälönä. Häviöttömälle aaltoputkelle tämä ominaisyhtälö sieventyy muotoon:

$\beta _{g}=\pm {\sqrt {\omega ^{2}\mu \epsilon -k_{c}^{2}}}$

(eq.68)

Tämän Besselin yhtälön ratkaisut ovat:

$R=C_{n}J_{n}\left(k_{c}r\right)+D_{n}N_{n}\left(k_{c}r\right)\,$

(eq.69)

missä $J_{n}\left(k_{c}r\right)\,$ on n:nnen kertaluokan ensimmäisen tyypin Besselin funktio joka kuvaa putken sisällä seisovaa aaltoa $\cos \left(k_{c}r\right)$ r:n arvoilla nollasta a:han. Samaan tapaan $N_{n}\left(k_{c}r\right)\,$ on n:nen kertaluvin toisen tyypin Besselin funktio joka kuvaa seisovaa aaltoa: $\sin \left(k_{c}r\right)\,$ r:n ollessa a:ta suurempi.

Näin saamme Helmholtzin yhtälön ratkaisuksi sylinterikoordinaateissa:

$\Psi =\left(C_{n}J_{n}\left(k_{c}r\right)+D_{n}N_{n}\left(k_{c}r\right)\right)\left(A_{n}\sin n\phi +B_{n}\cos n\phi \right)e^{\pm \beta _{g}z}$

(eq.70)

Kuitenkin kun $r=0\,$, on $k_{c}r=0\,$ ja funktio $N_{n}\,$ lähestyy ääretöntä ja siksi $D_{n}=0$. Tästä kaikesta seuraa, että z-akselilla kentän täytyy olla äärellinen.

Tekemällä lisää trigonometrista jumppaa, saamme (eq.70):n sin/cos termeistä:

$\left(A_{n}\sin n\phi +B_{n}\cos n\phi \right)\,$	$={\sqrt {A_{n}^{2}+B_{n}^{2}}}\cos \left(n\phi +\arctan {\frac {A_{n}}{B_{n}}}\right)$
	$=F_{n}\cos n\phi \,$	(eq.71)

josta edelleen Helmholtzin yhtälö pelkistyy:

$\Psi =\Psi _{0}\,J_{n}\left(k_{c}r\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}\,$

(eq.72)

TE-aaltoputkimoodit pyöreälle putkelle

Katsotaan tilannetta, jossa aalto etenee putkessa positiiviseen z-akselin suuntaan edellä esitellyin koordinaatein.

Pyöreän aaltoputken TE_np-moodeille tunnusomaista on, että $E_{z}=0.\,$ Tämä tarkoittaa, että magneettikentän $H_{z}\,$ z-komponentin pitää olla olemassa jotta putkessa esiintyy energian siirtoa. Helmholtzin yhtälö $H_{z}\,$:lle sylinterimäisessä putkessa on lausuttavissa:

$\nabla ^{2}H_{z}=\gamma ^{2}H_{z}$

(eq.73)

sen ratkaisu on yhtälön (eq.72) mukaan:

$H_{z}=H_{0z}J_{n}\left(k_{c}r\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}\,$

(eq.74)

joihin vaikuttavat vielä reunaehdot..

Häviöttömälle eristeaineelle (tyhjölle), Maxwellin curl-yhtälöt taajuus-domainissa ovat:

$\nabla \times \mathbf {E} =\,$	$-j\omega \mu \mathbf {H} \,$	(eq.75-H)
$\nabla \times \mathbf {H} =\,$	$j\omega \epsilon \mathbf {E} \,$	(eq.75-E)

Sylinterikoordinaateissa näiden komponenttiesitys on:

${\frac {1}{r}}{\frac {\partial E_{z}}{\partial \phi }}-{\frac {\partial E_{\phi }}{\partial z}}=$	$-j\omega \mu H_{r}\,$	(eq.76-Hr)
${\frac {\partial E_{r}}{\partial z}}-{\frac {\partial E_{z}}{\partial r}}=$	$-j\omega \mu H_{\phi }\,$	(eq.76-Hp)
${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rE_{\phi }\right)-{\frac {1}{r}}{\frac {\partial E_{r}}{\partial \phi }}=$	$-j\omega \mu H_{z}\,$	(eq.76-Hz)
${\frac {1}{r}}{\frac {\partial H_{z}}{\partial \phi }}-{\frac {\partial H_{\phi }}{\partial z}}=$	$j\omega \epsilon E_{r}\,$	(eq.76-Er)
$-j\beta _{g}H_{r}-{\frac {\partial H_{z}}{\partial r}}=$	$j\omega \epsilon E_{\phi }\,$	(eq.76-Ep)
${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rH_{\phi }\right)-{\frac {1}{r}}{\frac {\partial H_{r}}{\partial \phi }}=$	$j\omega \epsilon E_{z}\,$	(eq.76-Ez)

Kun differentiaatio $\partial /\partial z\,$ korvataan $\left(-j\beta _{g}\right)\,$ ja sähkökentän z-komponentti $E_{z}\,$ nollalla, sekä tehdään sijoitus $k_{c}^{2}=\omega ^{2}\mu \epsilon -\beta _{g}^{2}\,$, saadaan TE-moodin yhtälöt pyöreässä aaltoputkessa $H_{z}\,$:n suhteen lausuttuna:

$E_{r}=\,$	$-\,$	${\frac {j\omega \mu }{k_{c}^{2}}}{\frac {1}{r}}{\frac {\partial H_{z}}{\partial \phi }}$	(eq.77-Er)
$E_{\phi }=\,$		${\frac {j\omega \mu }{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial r}}$	(eq.77-Ep)
$E_{z}=\,$		$0\,$	(eq.77-Ez)
$H_{r}=\,$		${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial H_{z}}{\partial r}}$	(eq.77-Hr)
$H_{\phi }=\,$		${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {1}{r}}{\frac {\partial H_{z}}{\partial \phi }}$	(eq.77-Hp)
$H_{z}=\,$		$H_{0z}J_{n}\left(k_{c}r\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.77-Hz)

Aaltoputkessa yhtälöiden ratkaisuissa putken sisäpinnalla pitää sähkökentän $\phi \,$ komponentin $E_{\phi }\,$ kadota, tai että magneettikentän r-komponentin $H_{r}\,$ pitää kadota. Näinollen:

$E_{\phi }=0,\,$	kun	$r=a\,$		$\Rightarrow \left.{\frac {\partial H_{z}}{\partial r}}\right|_{r=a}=0$
$H_{r}=0,\,$	kun	$r=a\,$		$\Rightarrow \left.{\frac {\partial H_{z}}{\partial r}}\right|_{r=a}=0$

Tämä ehto voidaan lausua myös yhtälön (eq.74) tapaan muodossa:

$\left.{\frac {\partial H_{z}}{\partial r}}\right|_{r=a}=H_{0z}J_{n}^{\prime }\left(k_{c}a\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}=0$

(eq.78)

ja siinä nimenomaan:

$J_{n}^{\prime }\left(k_{c}a\right)=0\,$

(eq.79)

missä $J_{n}^{\prime }\,$ on $J_{n}\,$:n derivaatta.

Koskapa $J_{n}\,$ on oskilloiva funktio, myös $J_{n}^{\prime }\left(k_{c}a\right)\,$ on oskilloiva. Tästä seuraa, että on olemassa ääretön määrä $\left(k_{c}a\right)\,$ arvoja, jotka toteuttavat yhtälön (eq.78) ehdon. Nämä pisteet ovat paikallisia maksimeja ja minimejä Besselin funktiolla.

p:nnes nolla $J_{n}^{\prime }\left(k_{c}a\right)\,$ TE_np moodeille

p	n=	0	1	2	3	4	5
1		3.832	1.841	3.054	4.201	5.317	6.416
2		7.016	5.331	6.706	8.015	9.282	10.520
3		10.173	8.536	9.969	11.346	12.682	13.987
4		13.324	11.706	13.190

Koska pienin arvo on moodilla TE₁₁, se on pyöreän aaltoputken dominoiva TE-moodi. Kuten myöhemmin näemme, TM-moodien pienin indeksi on tätä suurempi ja siksi tämä TE-moodi on myös pyöreän aaltoputken dominoiva moodi.

Kirjoittamalla $k_{c}\,$:n arvot muotoon:

$k_{c}={\frac {X_{np}^{\prime }}{a}}$

(eq.80)

Sijoittamalla yhtälö (eq.74) yhtälöihin (eq.77), sekä käyttämällä ekvivalenttiutta: $Z_{g}=E_{r}/H_{\phi }=-E_{\phi }/H_{r},\,$ saamme:

$E_{r}=\,$		$E_{0r}J_{n}\left({\frac {X_{np}^{\prime }r}{a}}\right)\sin \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.81-Er)
$E_{\phi }=\,$		$E_{0r}J_{n}^{\prime }\left({\frac {X_{np}^{\prime }r}{a}}\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.81-Ep)
$E_{z}=\,$		$0\,$	(eq.81-Ez)
$H_{r}=\,$	$-\,$	${\frac {E_{0\phi }}{Z_{g}}}J_{n}^{\prime }\left({\frac {X_{np}^{\prime }r}{a}}\right)\cos \left(n\phi \right)e^{j\beta _{g}z}$	(eq.81-Hr)
$H_{\phi }=\,$		${\frac {E_{0r}}{Z_{g}}}J_{n}\left({\frac {X_{np}^{\prime }r}{a}}\right)\sin \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.81-Hp)
$H_{z}=\,$		$H_{0z}J_{n}\left({\frac {X_{np}^{\prime }r}{a}}\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.81-Hz)

edellä n = 0, 1, 2, 3, ... ja p = 1, 2, 3, 4, ...

Moodin ensimmäinen indeksi n esittää täysiä kenttävoimakkuuden muutosjaksoja täyden poikittaisen kierroksen matkalla. Toinen indeksi p kertoo säteittäisen sähkökentän nollien määrän ja jos z-akselille tarjotaan nollaa, sitä ei hyväksytä.

Vaihenopeus putken sisällä olevassa eristeaineessa:

$v_{p}={\frac {1}{\sqrt {\mu \epsilon }}}={\frac {c}{\sqrt {\mu _{r}\epsilon _{r}}}}$

(eq.82)

joka ilmalle/tyhjölle on käytännössä valonnopeus.

Etenemisvakiota määrittävät ryhmän (eq.77) yhtälöt ja se on:

$\beta _{g}={\sqrt {\omega ^{2}\mu \epsilon -\left({\frac {X_{np}^{\prime }}{r}}\right)^{2}}}$

(eq.83)

Cutoff wave number on sellainen, missä moodin etenemisvakio katoaa:

$k_{c}={\frac {X_{np}^{\prime }}{r}}=\omega _{c}{\sqrt {\mu \epsilon }}={\frac {\omega _{c}}{v_{p}}}$

(eq.84)

Alarajataajuus on puolestaan:

$f_{c}={\frac {X_{np}^{\prime }}{2\pi r{\sqrt {\mu \epsilon }}}}={\frac {X_{np}^{\prime }v_{p}}{2\pi r}}$

(eq.85)

sitä vastaava aallonpituus:

$\lambda _{c}={\frac {2\pi r}{X_{np}^{\prime }}}$

(eq.85)

Huomio: Tämä ei riipu putken täyteaineen ominaisuuksista!

TE-moodin vaihenopeus:

$v_{g}={\frac {\omega }{\beta _{g}}}={\frac {v_{p}}{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.86)

Aallonpituus:

$\lambda _{g}={\frac {\lambda }{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.87)

jossa $\lambda ={\frac {v_{p}}{f}}$ on aallonpituus täytteenä olevassa eristeaineessa.

Aaltoimpedanssi:

$Z_{g}={\frac {\omega \mu }{\beta _{g}}}={\frac {\eta }{\sqrt {1-\left(f_{c}/f\right)^{2}}}}$

(eq.88)

missä $\eta ={\sqrt {\mu /\epsilon }}$ on eristeaineen ominaisimpedanssi.

TM-aaltoputkimoodi pyöreälle putkelle

Seuraavaksi tarkastellaan tilannetta, jossa magneettikenttä on etenemäsuuntaan nähden poikittainen, Transverse Magnetic eli TM.

Pyöreässä aaltoputkessa TM_np-moodin ominaispiirteenä on: $H_{z}=0\,$. Samanaikaisesti sähkökentän z-komponentin pitää poiketa nollasta, jotta aaltoputkessa tapahtuu energian siirtoa. Tästä seuraten saamme Helmholtzin yhtälön $E_{z}\,$ komponentille muotoon:

$\nabla ^{2}E_{z}=\gamma ^{2}E_{z}\,$

(eq.89)

sille saadaan yhtälön (eq.72) mukaan ratkaisuksi:

$E_{z}=E_{0z}J_{n}\left(k_{c}r\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}\,$

(eq.90)

jota rajoittavat muutamat reunaehdot, mm. että sähkökentän tangenttiaalinen komponentti katoaa aaltoputken sisäpinnalla, eli: $E_{z}=0,\,$ kun $r=a.\,$ Tästä seuraa, että:

$J_{n}\left(k_{c}a\right)=0\,$

(eq.91)

Koskapa $J_{n}\left(k_{c}r\right)\,$ on oskilloivien funktioiden joukko, sille on olemassa ääretön määrä ratkaisuja (juuria). Muutamia alkupään juuria tarjotaan oheisessa taulukossa:

p:nnes nolla $J_{n}\left(k_{c}a\right)\,$ TM_np moodeille

p	n=	0	1	2	3	4	5
1		2.405	3.832	5.136	6.380	7.588	8.771
2		5.520	7.106	8.417	9.761	11.065	12.339
3		8.645	10.173	11.620	13.015	14.372
4		11.792	13.324	14.796

Näistä arvoista pienin on moodilla, TM₀₁ joka on siten TM-moodeista dominoiva, mutta on silti isompi, kuin TE-moodin pienin ja siten ei ole aaltoputken dominoiva moodi.

Ehdolla $H_{z}=0\,$ ja $\partial /\partial z=-j\beta _{g}\,$ pyöreän aaltoputken kenttäyhtälöistä muodostuu sijoitusten $\nabla \times \mathbf {E} =-j\omega \mu \mathbf {H} ,\,$ $\nabla \times \mathbf {H} =j\omega \epsilon \mathbf {E} \,$ ja $k_{c}^{2}=\omega ^{2}\mu \epsilon -\beta _{g}^{2}\,$ jälkeen:

$E_{r}=\,$		${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial r}}$	(eq.92-Er)
$E_{\phi }=\,$		${\frac {-j\beta _{g}}{k_{c}^{2}}}{\frac {1}{r}}{\frac {\partial E_{z}}{\partial \phi }}$	(eq.92-Ep)
$E_{z}=\,$		$E_{0z}J_{n}\left(k_{c}r\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}\,$	(eq.92-Ez)
$H_{r}=\,$		${\frac {j\omega \epsilon }{k_{c}^{2}}}{\frac {1}{r}}{\frac {\partial E_{z}}{\partial \phi }}$	(eq.92-Hr)
$H_{\phi }=\,$	$-\,$	${\frac {j\omega \epsilon }{k_{c}^{2}}}{\frac {\partial E_{z}}{\partial \phi }}$	(eq.92-Hr)
$H_{z}=\,$		$0\,$	(eq.92-Hz)

Differentoimalla yhtälö (eq.90) z:n suhteen ja sijoittamalla tulos yhtälöryhmään (eq.91), sekä tekemällä sijoitukset: $Z_{g}=E_{r}/H_{\phi }=-E_{\phi }/H_{r}=\beta _{g}/\omega \epsilon ,\,$ $k_{c}=X_{np}/a\,$, sekä missä n = 0, 1, 2, 3, ... ja p = 1, 2, 3, 4, ... saadaan pyöreän aaltoputken TM_np-moodin kenttäyhtälöiksi:

$E_{r}=\,$	$E_{0r}J_{n}^{\prime }\left({\frac {X_{np}r}{a}}\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.93-Er)
$E_{\phi }=\,$	$E_{0\phi }J_{n}\left({\frac {X_{np}r}{a}}\right)\sin \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.93-Ep)
$E_{z}=\,$	$E_{0z}J_{n}\left({\frac {X_{np}r}{a}}\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.93-Ez)
$H_{r}=\,$	${\frac {E_{0\phi }}{Z_{g}}}J_{n}\left({\frac {X_{np}r}{a}}\right)\sin \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.93-Hr)
$H_{\phi }=\,$	${\frac {E_{0r}}{Z_{g}}}J_{n}^{\prime }\left({\frac {X_{np}r}{a}}\right)\cos \left(n\phi \right)e^{-j\beta _{g}z}$	(eq.93-Hp)
$H_{z}=\,$	$0\,$	(eq.93-Hz)

Useimmat TM-moodin ominaisyhtälöistä ovat identtisiä TE-moodin kanssa, mutta jotkin eivät ole. Seuraavassa esitellään kaikki eroavat:

Apumuuttujana käytettävä vaihenopeus putken sisällä olevassa eristeaineessa:

$v_{p}={\frac {1}{\sqrt {\mu \epsilon }}}={\frac {c}{\sqrt {\mu _{r}\epsilon _{r}}}}$

joka ilmalle/tyhjölle on käytännössä valonnopeus.

Etenemisvakio on muotoa: (vertaa eq.83)

$\beta _{g}={\sqrt {\omega ^{2}\mu \epsilon -\left({\frac {X_{np}}{r}}\right)^{2}}}$

(eq.94)

Cutoff wave number on sellainen, missä etenemisvakio katoaa (nollaan):

$k_{c}={\frac {X_{np}}{r}}=\omega _{c}{\sqrt {\mu \epsilon }}={\frac {\omega _{c}}{v_{p}}}$

(eq.95)

Moodin alarajataajuus:

$f_{c}={\frac {X_{np}}{2\pi r{\sqrt {\mu \epsilon }}}}={\frac {X_{np}v_{p}}{2\pi r}}$

(eq.96)

sitä vastaava aallonpituus:

$\lambda _{c}={\frac {2\pi r}{X_{np}}}$

(eq.97)

Huomio: Tämä ei riipu putken täyteaineen ominaisuuksista!

TM-moodin vaihenopeus $v_{g}\,$ on sama yhtälö, kuin TE-moodilla. (eq.86)

Aallonpituus $\lambda _{g}\,$ on sama yhtälö, kuin TE-moodilla. (eq.87)

Aaltoimpedanssi $Z_{g}$ on sama yhtälö, kuin TE-moodilla. (eq.88)

TEM-moodit pyöreässä aaltoputkessa

Moodi jossa sekä sähkö- että magneettikentät ovat poikittaisia (transverse electric and transverse magnetic: TEM) tunnetaan myös siirtolinjamoodeina ja sen tuntomerkki on:

$E_{z}=H_{z}=0\,$

Tässä tilanteessa sekä sähkökenttä, että magneettikenttä on poikittainen suhteessa etenemäsuuntaan, eikä sellainen moodi voi esiintyä ontossa aaltoputkessa. Sen sijaan se esiintyy koaksiaalisessa siirtolinjassa tai parijohdossa. TEM-moodin analyysi esittää erinomaisesti piiriteorian ja kenttäteorian analogisuuden.

Käytettävä koordinaattijärjestelmä koaksiaalijohdon analyysissä:

• $\phi \,$ (fii): x-y -tason origon ympäri x-akselista laskettava kulma
• r: Etäisyys z-akselista
• a: ulkojohtimen sisäpinnan säde
• b: sisäjohtimen ulkopinnan säde
• z: z-koordinaatti, l. etäisyys x-y-tasosta.

Maxwellin curl-yhtälöt sylinterimäisissä koordinaateissa:

$\nabla \times \mathbf {E} =\,$	$-\,$	$j\omega \mu \mathbf {H} \,$	(eq.98-H)
$\nabla \times \mathbf {H} =\,$		$j\omega \epsilon \mathbf {E} \,$	(eq.98-E)

tekemällä sijoitukset $\partial /\partial r=-j\beta _{g}\,$ ja $E_{z}=H_{z}=0\,$ saadaan:

$B_{g}E_{r}=\,$		$\omega \mu H_{\phi }\,$	(eq.99-Hp)
$B_{g}E_{\phi }=\,$		$\omega \mu H_{r}\,$	(eq.99-Hr)
${\frac {\partial }{\partial r}}\left(rE_{\phi }\right)=$		$0\,$	(eq.99-Hz)
$\beta _{g}H_{r}=\,$	$-\,$	$\omega \epsilon E_{\phi }\,$	(eq.99-Ep)
$\beta _{g}H_{\phi }=\,$		$\omega \epsilon E_{r}\,$	(eq.99-Er)
${\frac {\partial }{\partial r}}\left(rH_{\phi }\right)-{\frac {\partial H_{r}}{\partial \phi }}=$		$0\,$	(eq.99-Ez)

Sijoittamalla yhtälö (eq.99-Hr) yhtälöön (eq.99-Ep) saadaan koaksiaalin TEM-moodin etenemisvakio:

$\beta _{g}=\omega {\sqrt {\mu \epsilon }}$

(eq.100)

Vertaamalla edellä saatua yhtälöä pyöreän aaltoputken yhtälön (eq.68) kanssa:

$\beta _{g}^{2}=\omega \mu \epsilon -k_{c}^{2}\,$

(eq.101)

havaitaan, että:

$k_{c}=0\,$

(eq.102)

joka merkitsee, että TEM-moodin alarajataajuus koaksiaalilinjalle on nolla, joka on sama kuin tavallisella siirtolinjalla.

TEM-moodin vaihenopeus voidaan lausua yhtälöllä (eq.100) muodossa:

$v_{p}={\frac {\omega }{\beta _{g}}}={\frac {1}{\sqrt {\mu \epsilon }}}$

(eq.103)

joka valonnopeus kaapelin eristeessä.

TEM-moodin aaltoimpedanssi löytyy joko yhtälöillä (eq.99-Hp) ja (eq.99-Ep), tai (eq.99-Hr) ja (eq.99-Er) muodossa:

$\eta \left(\mathrm {TEM} \right)={\sqrt {\mu /\epsilon }}\,$

(eq.104)

joka on kaapelin eristeaineen aaltoimpedanssi.

Ampèren laki lausii, että magneettikentän H viivaintegraali mitä tahansa suljettua viivaa pitkin on täsmälleen yhtäsuuri, kuin sen viivan sisäänsä sulkema virta, eli:

$\oint \mathbf {H} \;\cdot \;d\ell =I=I_{0}e^{-j\beta _{g}z}=2\pi rH_{\phi }\,$

(eq.104)

missä I on kompleksinen virta, jota tukemaan tarvitaan koaksiaalin keskijohdin.

Yhteen vetona TEM-moodin ominaisuudet häviöttömässä eristeessä ovat:

1. Alarajataajuus on nolla
2. Sitä kuljettava siirtolinja on kaksijohteinen järjestelmä
3. Sen aaltoimpedanssi on eristeaineen impedanssi
4. Sen etenemisvakio on eristeaineen etenemisvakio
5. Sen vaihenopeus on valonnopeus eristeaineessa.

Tehon kulkeminen pyöreässä aaltoputkessa tai koaksiaalilinjassa

Kuten suorakulmaistenkin aaltoputkien tapauksessa, on tehon kulkeminen laskettavissa pyöreissä aaltoputkissa Poynting teoreemalla. Häivöttömälle eristeelle aikakeskiarvotettu tehonsiirto pyöreässä aaltoputkessa saadaan muotoon:

$P_{tr}={\frac {1}{2Z_{g}}}\int _{0}^{2\pi }\int _{0}^{a}\left(\left|E_{r}\right|^{2}+\left|E_{\phi }\right|^{2}\right)r\;dr\;d\phi$	(eq.105)
$P_{tr}={\frac {Z_{g}}{2}}\int _{0}^{2\pi }\int _{0}^{a}\left(\left|H_{r}\right|^{2}+\left|H_{\phi }\right|^{2}\right)r\;dr\;d\phi$	(eq.106)

missä $Z_{g}=E_{r}/H_{\phi }=-E_{\phi }/H_{r}\,$ = johteen aaltoimpedanssi, ja a = aaltoputken säde.

Sijoittamalla $Z_{g}\,$ kiinnostuksen kohteena olevalle moodille yhtälöön (eq.105) saadaan putkessa sillä moodilla kulkeva teho.

TE_np-moodeille keskimääräinen aaltoputken läpi kuljetettu teho on:

$P_{tr}={\frac {\sqrt {1-\left(f_{c}/f\right)^{2}}}{2\eta }}\int _{0}^{2\pi }\int _{0}^{2}\left(\left|E_{r}\right|^{2}+\left|E_{\phi }\right|^{2}\right)r\;dr\;d\phi$

(eq.107)

missä $\eta ={\sqrt {\mu /\epsilon }}\,$ on sisäeristeen ominaisimpedanssi.

TM_np-moodeille keskimääräinen aaltoputken läpi kuljetettu teho on:

$P_{tr}={\frac {1}{2\eta {\sqrt {1-\left(f_{c}/f\right)^{2}}}}}\int _{0}^{2\pi }\int _{0}^{2}\left(\left|E_{r}\right|^{2}+\left|E_{\phi }\right|^{2}\right)r\;dr\;d\phi$

(eq.108)

TEM-moodeilla keskimääräinen teho koaksiaalilinjan, tai avoparijohdon läpi on:

$P_{tr}={\frac {1}{2\eta }}\int _{0}^{2\pi }\int _{0}^{2}\left(\left|E_{r}\right|^{2}+\left|E_{\phi }\right|^{2}\right)r\;dr\;d\phi$

(eq.109)

Merkitsemällä koaksiaalin keskijohtimen kautta kulkevaa virtaa:

$I_{z}=I_{0}e^{-j\beta _{g}z}\,$

(eq.110)

saadaan johtimen ympärillä olevan magneettikentän voimakkuudeksi Ampèren lain mukaan:

$H_{\phi }={\frac {I_{0}}{2\pi r}}e^{-j\beta _{g}z}\,$

(eq.111)

Potentiaaliero ulkojohtimesta keskijohtimeen on:

$V_{r}=-\int _{b}^{a}E_{r}dr=-\int _{b}^{a}\eta H_{\phi }dr={\frac {I_{0}\eta }{2\pi }}\ln \left({\frac {a}{b}}\right)e^{-j\beta _{g}z}\,$

(eq.112)

Koaksiaalilinjan ominaisimpedanssi on:

$Z_{0}={\frac {V}{I}}={\frac {\eta }{2\pi }}\ln \left({\frac {b}{a}}\right)\,$

(eq.113)

missä $\eta ={\sqrt {\mu /\epsilon }}$ on eristeaineen ominaisimpedanssi.

TEM-moodeilla koaksiaalilinjaa pitkin kulkeva teho on yhtälön (eq.109) mukaan:

$P_{tr}={\frac {1}{2\eta }}\int _{0}^{2\pi }\int _{a}^{b}\left|\eta H_{\phi }\right|^{2}\;r\;dr\;d\phi ={\frac {\eta I_{0}^{2}}{4\pi }}\ln \left({\frac {b}{a}}\right)$

(eq.114)

Sijoittamalla $\left|V_{r}\right|\,$ yhtälöstä (eq.112) yhtälöön (eq.114) saadaan:

$P_{tr}={\frac {1}{2}}V_{0}I_{0}$

(eq.115)

Tehohäviöt pyöreässä aaltoputkessa tai koaksiaalilinjassa

Teoria ja yhtälöt jotka on edellä johdettu TE- ja TM-moodeille suorakulmaisessa putkessa toimivat myös pyöreässä putkessa. Tehohäviöt TEM-moodisessa koaksiaalisessa linjassa voidaan laskea siirtolinjateorialla muotoon:

$P_{L}=2\alpha P_{tr}\,$

(eq.116)

missä:

• $P_{L}\,$ = tehohäviö pituusyksikköä kohti
• $P_{tr}\,$ = siirretty teho
• $\alpha \,$ = vaimennusvakio

Vähähäviöisille johtimille vaimennusvakio on muotoa:

$\alpha ={\frac {1}{2}}\left(R{\sqrt {\frac {C}{L}}}+G{\sqrt {\frac {L}{C}}}\right)\,$

(eq.117)